Elliptic curves

tl;dr: Everything I wanted to know, but was afraid to ask about elliptic curves.

History

Preliminaries

• finite fields $\Fq$ of prime order $q$
  • $e_*$ is the multiplicative identity element in $K$, typically denoted by 1
  • $e_+$ is the additive identity element in $K$, typically denoted by 0
  • the smallest $n>0$, such that $\underbrace{e_* + e_* + \cdots + e_*}_{n\ \text{times}} = e_+$ is called the field characteristic.
• TODO: (full?) algebraic closure of a finite field $K$
  • Example: for $\mathbb{Q}$, the full algebraic closure $\bar{\mathbb{Q}}$ includes $\sqrt{-2}$.
  • TODO: Clarify the difference between $K$ and $\bar{K}$ (the algebraic closure of $K$), because points on the curve come from the latter.
    • Wicher said it’s kind of like the real numbers: not every polynomial has a root in $\mathbb{R}$, so the algebraic closure of $\mathbb{R}$ are the complex numbers $\mathbb{C}$, where every polynomial has a root.
    • Somehow the “every polynomial has a root over $\bar{K}$” property is a useful one for algebraic geometry / elliptic curves in particular
• TODO: $\mathbb{A}^n(K)$ = affine $n$-spaces over field $K$
• TODO: quadratic extension $\F_{q^2} = \Fq(i)$ with $i^2 + 1 = 0$

A few notes

The general Weierstrass equation:

\begin{align} \label{eq:general-weierstrass} E : y^2 + a_1 xy + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6 \end{align}

The short Weierstrass equation: \begin{align} \label{eq:short-weierstrass} E : y^2 = x^3 + a x + b \end{align}

How? Assume the field characteristic is not 2 or 3.

Why? I think it’s to allow for the few substitutions below to simplify into short Weierstrass…)

Then, with a few substitutions, we arrive at Equation $\ref{eq:short-weierstrass}$.

If $(a_1, \ldots, a_6)$ come from $K$, then $E$ is said to be defined over $K$, which is denoted as $E / K$.

An elliptic curve group (over a field $K$) is defined as: \begin{align} E(K) = \{(x,y)\in \mathbb{A}^2(K) : y^2 = x^3 + ax + b\} \cup \{\ecid\} \end{align}

Here, $\ecid$ denotes the identity element of $E(K)$, also called the point at infinity. Note that $\ecid$ is a “special case” point that is defined artificially; it does not have any $(x,y)$ coordinates (as we’ll see later).

Note that we typically just have $(x,y)\in K^2$?

$E = E(\bar{K})$ is typically used to refer to the same group defined over the full algebraic closure of $K$. (e.g., when $K = \mathbb{Q}$, $\bar{K}$ is $\mathbb{R}$)

We’ll initially denote the elliptic curve group operation by $\oplus$ (and its inverse by $\ominus$), but at a later point we will replace it with $+$ (and $-$, respectively).

Note that the identity element of $E(K)$ denoted by $\ecid$ is a “special case” point; it is defined artificially.

For any $P\in E(K)$, we denote $\underbrace{P \oplus P \oplus \cdots \oplus P}_{n\ \text{times}} \bydef [n]P$.

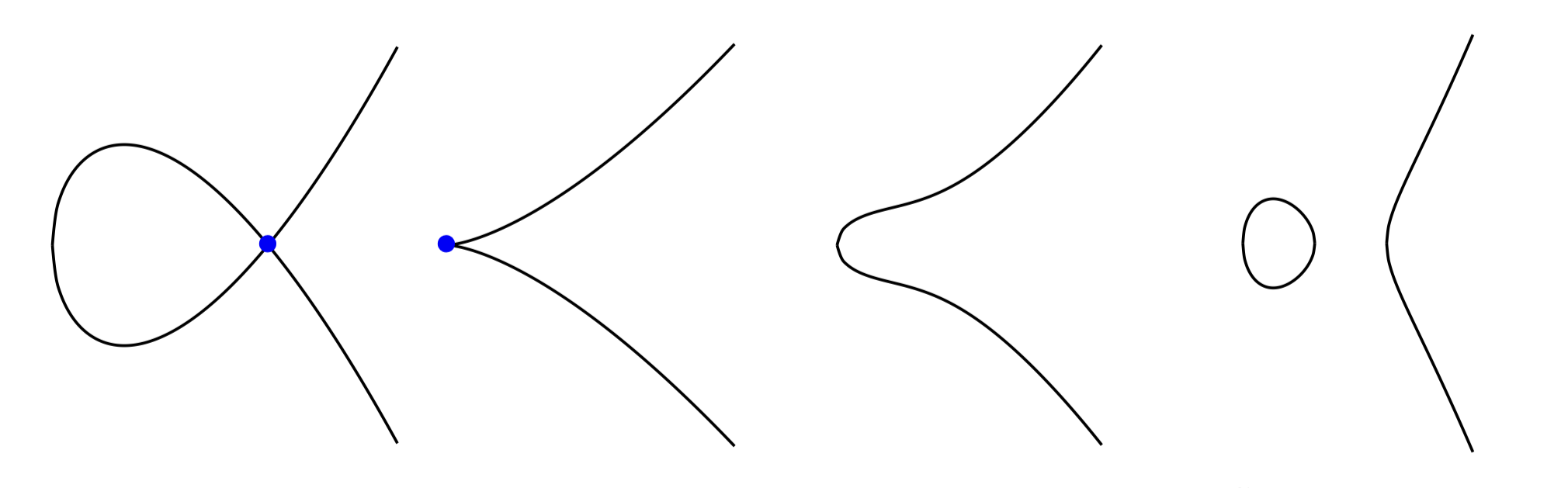
A note on (non)singular elliptic curves, whose future relevance I am unsure of. Q: Why are singular curves bad?

TODOs

• explain group addition law; plus, link to picture
• Why is the 3rd intersection point flipped over (“reflected”) in the additional law? Would DL be easy w/o that?
• Affine vs. projective coordinates
• group axioms
  • closure, by virtue of R being the third root of the cubic polynomial (whose first two roots were the points P and Q)
  • associativity
• weirstrass model is not ideal for fast impl. of the group addition law
  • projective coordinates avoid inversions (may be worth only mentioning it? cause lots of details to cover)
  • jacobi quartic form (just mention it; too advanced for now)
• the order of $E(\Fq)$
• Hasse bound
• the CM algorithm

Acknowledgements

Most screenshots in this post (and most of my understanding of elliptic curves) come from Craig Costello’s “Pairings for beginners.”¹.

Thanks to Wicher Malten for reminding me what an algebraic closure is.

---