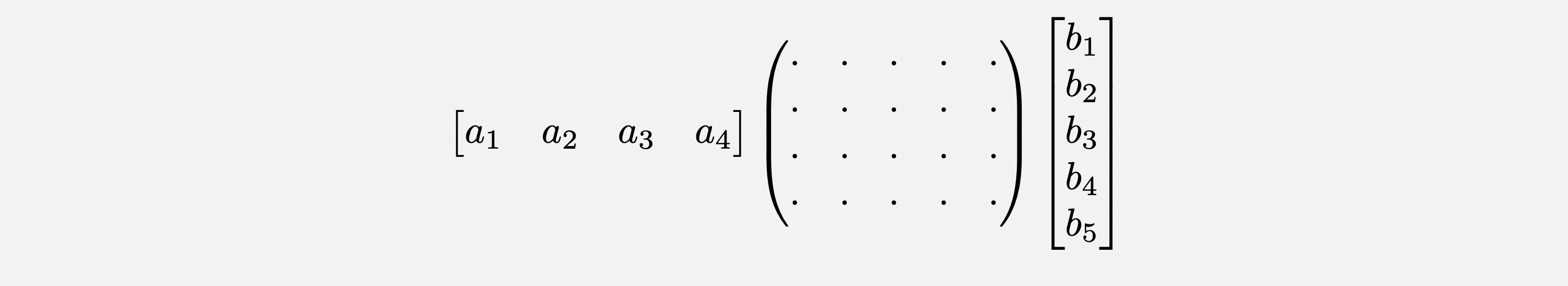Hyrax polynomial commitment scheme

tl;dr: Hyrax is polynomial commitment scheme (PCS) with (1) sublinear commitment-and-proof sizes and (2) sublinear opening-and-verification times. Hyrax is constructed from Pedersen vector commitments and Bulletproofs inner product arguments (IPAs). Hyrax has information-theoretic hiding commitments and honest verifier zero-knowledge (HVZK) PCS openings.

Preliminaries

• For time complexities, we use:
  • $\Fadd{n}$ for $n$ field additions in $\F$

  • $\Fmul{n}$ for $n$ field multiplications in $\F$

  • $\msm{n}$ for a single multi-scalar multiplication (MSM) in $\Gr$ of size $n$

  • $\fmsm{n}{< B}$ for a single multi-scalar multiplication (MSM) in $\Gr$ of size $n$ where the group element bases are known ahead of time (i.e., fixed-base) and each scalar is $< B$
  • $\vmsm{n}{< B}$ for a single multi-scalar multiplication (MSM) in $\Gr$ of size $n$ where the group element bases are NOT known ahead of time (i.e., variable-base) and each scalar is $< B$
• Multilinear extensions (MLEs)
• The finite field $\F$ is of prime order $p$

Overview

The main idea in Hyrax is that, for a row vector $\term{\a}\in\F^{1\times n}$, a column vector $\term{\b}^\top \in \F^m$ and a matrix $\term{\mat{A}}\in \F^{n\times m}$, you can express a dot product as: \begin{align} \label{eq:hyrax} \sum_{i\in[n), j\in[m)} a_i \cdot M_{i,j} \cdot b_j = \emph{\a\cdot \mat{M}\cdot \b^\top} &\bydef \underbrace{\a}_{\in\F^{1\times n}} \cdot \underbrace{\begin{bmatrix} \mat{M}_0 \cdot \b^\top\\
\mat{M}_1 \cdot \b^\top\\
\vdots &\\
\mat{M}_{n-1} \cdot \b^\top\\
\end{bmatrix}}_{\in \F^n}\\
%\label{eq:hyrax-rows} &\bydef \underbrace{\begin{bmatrix} %| & | & & |\\
\a \cdot \mat{M}_0^\top & \a \cdot \mat{M}_1^\top & \cdots & \a \cdot \mat{M}_{m-1}^\top\\
%| & | & & |\\
\label{eq:hyrax-cols} \end{bmatrix}}_{\in\F^{1\times m}}\cdot\underbrace{\b^\top}_{\in\F^m} \end{align} where $\term{\mat{M}_i}\in\F^{1\times m}$ is the $i$th row in $\mat{M}$ and $\term{\mat{M}^\top_j}\in\F^n$ is the $j$th column.

Hyrax represents an MLE $\term{f(\X,\Y)}\in \MLE{n,m}$ as a matrix $\mat{M}$, where each row $\emph{\mat{M}_i} \bydef (f(\i,\j))_{j\in[m)}$. Put differently, $\term{M_{i,j}}\bydef f(\i,\j)$.

Hyrax commits to $f$ by individually committing to the rows $\mat{M}_i$ using a hiding Pedersen vector commitment as: \begin{align} \term{C_i} \gets \term{r_i} \cdot \term{H} + \mat{M}_i \cdot \term{\G} = r_i\cdot H+ \sum_{j\in[m)} f(\i, \j) \cdot G_j\in \Gr \end{align} where $\emph{\G,H}\in\Gr^{m+1}$ is the commitment key and $r_i\randget \F$. This yields an $n$-sized commitment $\C\bydef(C_i)_{i\in[n)}$.

An opening proof for $z\equals f(\x,\y)$, can be framed through the lens of Eq. \ref{eq:hyrax}: \begin{align} z &=\sum_{i\in[n), j\in[m)} \eq(\x, \i) \cdot \eq(\y,\j) \cdot f(\i,\j)\\
&=\sum_{i\in[n), j\in[m)} \eq(\x, \i) \cdot M_{i,j} \cdot \eq(\y,\j)\\
&\bydef \sum_{i\in[n), j\in[m)} a_i \cdot M_{i,j} \cdot b_j =\a\cdot\mat{M}\cdot\b^\top \end{align} where $\a \bydef (\eq(\x,\i))_{i\in[n)}$ and $\b \bydef (\eq(\y, \j))_{j\in[m)}$.

What does an opening proof look like exactly?

First, both the prover and the verifier compute the $\a,\b$ vectors from $\x$ and $\y$.

Second, the verifier uses $\a$ and the $C_i$’s to derive a commitment $\term{D}$ to the vector $\a \cdot \mat{M} \in \F^{1\times m}$ from Eq. \ref{eq:hyrax-cols}: \begin{align} \term{D} \gets \sum_{i\in[n)} a_i\cdot D_i &= \sum_{i\in[n)} a_i\cdot(r_i \cdot H + \mat{M}_i\cdot \G)\\
&= \sum_{i\in[n)} (a_i\cdot r_i) \cdot H + \sum_{i\in[n)} a_i\cdot\left(\sum_{j\in[m)} M_{i,j} \cdot G_j\right)\\
&\bydef \term{u}\cdot H + \sum_{i\in[n)}\sum_{j\in[m)} (a_i\cdot M_{i,j}) \cdot G_j\\
&= u\cdot H + \sum_{j\in[m)}\left(\sum_{i\in[n)} (a_i\cdot M_{i,j})\right) \cdot G_j\\
&= u\cdot H + \sum_{j\in[m)}(\a\cdot \mat{M}^\top_j) \cdot G_j\\
\end{align} (This can be generalized into a nicer homorphic property of such Pedersen matrix commitments.)

Third, the prover computes $\a\cdot \mat{M}$ via $m$ inner-products in $\F$ of size $n$ each (as per Eq. \ref{eq:hyrax-cols}).

Fourth, the prover gives the verifier a size-$m$ inner-product argument (IPA) proof¹ that $z = (\a \cdot \mat{M})\cdot\b^\top$.

Lastly, the verifier checks the IPA proof against (1) the commitment $D$ to $\a\cdot{\mat{M}}$ and (2) $\b$.

To commit to MLEs $f\in\MLE{N}$, Hyrax is typically used with $n=m=\sqrt{N}$, yielding sublinear-sized commitments & proofs and sublinear-time verifier. The proving time will be dominated by the $\sqrt{N}$-sized IPA.

ZK construction

$\mathsf{Hyrax}_\mathsf{ZK}.\mathsf{Setup}(1^\lambda, \nu,\mu) \rightarrow (\mathsf{vk},\mathsf{ck})$

Notation:

• $n \gets 2^\nu$ denotes the # of matrix rows
• $m \gets 2^\mu$ denotes the # of matrix columns
• $N = n\cdot m\bydef 2^{\nu + \mu}$ denotes the total # of entries in the matrix

Pick random generators:

• $(\G,H)\randget\Gr^{m+1}$
• $\vk\gets (n, \G,H)$
• $\ck\gets \vk$

$\mathsf{Hyrax}_\mathsf{ZK}.\mathsf{Commit}(\mathsf{ck}, f(\boldsymbol{X},\boldsymbol{Y}); \r) \rightarrow (\boldsymbol{C},\aux)$

Let:

• $\emph{\mat{M}}\in\F^{n\times m}$ denote the matrix represention of the MLE $f$.

Compute the commitment:

• $(n,\G, H)\parse \ck$
• $C_i \gets r_i\cdot H + \mat{M}_i\cdot \G,\forall i\in[n)$
• $\aux \gets \r$

Computing each commitment takes an $\msm{m+1}\Rightarrow n\times\msm{m+1}$ in total. (Committing will be faster for sparse matrices, but in the Spartan setting, we don’t care about it.)

$\mathsf{Hyrax}_\mathsf{ZK}.\mathsf{Open}(\ck, f(\boldsymbol{X},\boldsymbol{Y}), (\boldsymbol{x}, \boldsymbol{y}), z; \aux, \C)\rightarrow \pi$

Parse commitment key and auxiliary data:

• $(n,\G,H)\parse \ck$
• $\r\gets\aux$

Compute the opening proof:

• $\a\gets (\eq(\x, \i))_{i\in[n)}\in\F^{1\times n}$
• $\b \gets (\eq(\y, \j))_{j\in[m)}\in \F^{1\times m}$
• $\A\gets \a\cdot \mat{M}\in \F^{1\times m}$
• $u\gets \sum_{i\in[n)} a_i\cdot r_i$
  • This will be the randomness for the commitment to $\A$, which the verifier will homomorphically-reconstruct
• $\pi \gets \ipaProve(\prk_\ipa, \A, \b, z; u)$ where $\prk_\ipa = (\G,H)$
  • This will be a ZK IPA proof that $z = \A\cdot \b^\top = \a\cdot\mat{M}\cdot\b^\top \bydef f(\x,\y)$

ZK opening time

First, recall that computing all Lagrange evaluations for a size-$n$ MLE takes $2n$ $\F$ multiplications.

• $\a$ takes $\Fmul{2n}$
• $\b$ takes $\Fmul{2m}$
• $\A$ takes $m \times(\Fmul{n}+\Fadd{n})=\Fmul{nm}+\Fadd{nm}$ because we are inner-producting $\a$ with every column $\mat{M}_j^\top\in\F^n$.
  • When the matrix is “sparse”, i.e., only has $\term{t}\bydef\sum_{j\in[m)} \term{t_j} \ll nm$ non-zero entries, with column $j$ having $\emph{t_j}$ non-zero entries, then this cost lowers to $\sum_{j\in[m)} (\Fmul{t_j}+\Fadd{t_j}) = \Fmul{t} + \Fadd{t}$
• $\vec{u}$ takes $\Fmul{n}+\Fadd{n}$
• $\pi$ takes $\term{\ipaProve(m)}$, which denotes the time of a size-$m$ IPA prover
  • e.g., $O(\Gmul{m})$ for Bulletproofs¹

In total, we have: \begin{align} &\underbrace{\Fmul{(2n + 2m)}}_{\a, \b} + \underbrace{(\Fmul{t} + \Fadd{t})}_{\A} + \underbrace{(\Fmul{n} + \Fadd{n})}_{\vec{u}} + \ipaProve(m)= \\
\def\zkopen{\Fmul{(3n + 2m + t)} + \Fadd{(t + n)} + \ipaProve(m)} = &\zkopen \end{align}

$\mathsf{Hyrax}_\mathsf{ZK}.\mathsf{Verify}(\vk, \boldsymbol{C}, (\boldsymbol{x}, \boldsymbol{y}), z; \pi)\rightarrow \{0,1\}$

• $(n,\G, H)\parse \vk$
• $\a\gets (\eq(\x, \i))_{i\in[n)}\in\F^{1\times n}$
• $\b \gets (\eq(\y, \j))_{j\in[m)}\in \F^{1\times m}$
• $D \gets \sum_{i\in[n)} a_i\cdot C_i$
  • This will be the Pedersen commitment to $\A\bydef\a\cdot\mat{M}$
• $\vk_\ipa\gets (\G,H)$
• assert $\ipaVer(\vk_\ipa, D, \b, z; \pi) \equals 1$

ZK verifier time

• $\a$ takes $\Fmul{2n}$ (recall from here)
• $\b$ takes $\Fmul{2m}$
• $D$ takes $\msm{n}$
• Verfiying $\pi$ takes $\term{\ipaVer(m)}$, which denotes the time of a size-$m$ IPA verifier (e.g., $O(\msm{m})$ for Bulletproofs¹)

In total, we have: \begin{align} \def\zkverify{\Fmul{2(n + m)} + \msm{n} + \ipaVer(m)} \zkverify \end{align}

ZK performance

We use $\hyraxZknm$ to refer to the $\hyraxZk$ scheme set up with $\hyraxZkSetup(1^\lambda, \log_2{n},\log_2{m})$. We use $\hyraxZkSqN$ to refer to $\hyraxZk^{\sqN,\sqN}$.

Setup, hiding commitments and ZK proof sizes

ZK openings at arbitry points

Recall that $\emph{t}\le nm$ denotes the # of non-zero entries in the MLE $f$ or, equivalently, matrix $\mat{M}$.

ZK openings at points on the hypercube

Non-ZK construction

$\mathsf{Hyrax}.\mathsf{Setup}(1^\lambda, \nu,\mu) \rightarrow (\mathsf{vk},\mathsf{ck})$

Pick random generators (reusing $\hyraxZk$ notation):

• $\G\randget\Gr^m$
• $\vk\gets (n, \G)$
• $\ck\gets \vk$

$\mathsf{Hyrax}.\mathsf{Commit}(\mathsf{ck}, f(\boldsymbol{X},\boldsymbol{Y})) \rightarrow \boldsymbol{C}$

Recall that $\mat{M}\in\F^{n \times m}$ represents the MLE $f\in\MLE(n,m)$.

• $(n,\G)\parse \ck$
• $C_i \gets \mat{M}_i\cdot \G,\forall i\in[n)$

Computing each commitment takes an $\msm{m}\Rightarrow n\times\msm{m}$ in total. (Committing will be faster for sparse matrices, but in the Spartan setting, we don’t care about it.)

$\mathsf{Hyrax}.\mathsf{Open}(\ck, f(\boldsymbol{X},\boldsymbol{Y}), (\boldsymbol{x}, \boldsymbol{y}), z; \C)\rightarrow \pi$

Parse commitment key:

• $(n,\G)\parse \ck$

Compute the opening proof:

• $\a\gets (\eq(\x, \i))_{i\in[n)}\in\F^{1\times n}$
• $\b \gets (\eq(\y, \j))_{j\in[m)}\in \F^{1\times m}$
• $\A\gets \a\cdot \mat{M}\in \F^{1\times m}$
• $\pi\gets \A$

A more succinct but less computationally-efficient variant, denoted by $\hyrax_\ipa$, would compute an IPA proof that $z = \A\cdot \b^\top$ instead of sending $\A$ over and having the verifier manually check.

Non-ZK opening time

• $\a$ takes $\Fmul{2n}$ (recall from here)
• $\b$ takes $\Fmul{2m}$
• $\A$ takes $\Fmul{nm}+\Fadd{nm}$ in the worst case, and $\Fmul{t}+\Fadd{t}$ in the sparse case with $\emph{t}$ non-zero entries in $\mat{M}$ (recall from here)

In total, we have $\Fmul{(2n + 2m + t)} + \Fadd{t}$ proving work for vanilla $\hyrax$. The $\hyrax_\ipa$ variant would require extra $\emph{\ipaProve(m)}$ work.

When $(\x,\y)$ are on the hypercube: (1) $\a$ and $\b$ are 0 everywhere except at location $x$ and $y$, and (2) $\A$ is just the $x$th row of $\mat{M}$. So opening time involves no computation. The proof remains the same size though.

$\mathsf{Hyrax}.\mathsf{Verify}(\vk, \boldsymbol{C}, (\boldsymbol{x}, \boldsymbol{y}), z; \pi)\rightarrow \{0,1\}$

• $(n,\cdot)\parse \vk$
• $\a\gets (\eq(\x, \i))_{i\in[n)}\in\F^{1\times n}$
• $\b \gets (\eq(\y, \j))_{j\in[m)}\in \F^{1\times m}$
• $D \gets \sum_{i\in[n)} a_i\cdot C_i$
  • This will be the Pedersen commitment to $\A\bydef\a\cdot\mat{M}\in\F^{1\times m}$
• $\A\parse \pi$
• assert $D\equals \A\cdot\vect{G}$
• assert $z\equals \A\cdot \b^\top$

The more succinct but less computationally-efficient $\hyrax_\ipa$ variant would verify an IPA proof instead of checking that $\A$ is committed in $D$ and manually re-computing $z$.

Non-ZK verifier time

• $\a$ takes $\Fmul{2n}$ (recall from here)
• $\b$ takes $\Fmul{2m}$
• $D$ takes $\vmsm{n}{< p}$ because:
  • the $a_i$ scalars are arbitrary $\eq(\x,\i)$ evaluations
  • the bases $C_i$ are the commitment which is not necessarily known ahead of time
• Verifying $\A$ against $D$ takes $\fmsm{m}{<p}$
  • the exponents in $\A$ will be arbitrary (see the opening algorithm)
  • the bases are fixed in the commitment key
• Although this last $D \equals \A \cdot \G$ check can be turned into a single $\msm{n+m}$ as $\left(\A\cdot (-\G)\right)\cdot \sum_{i\in[n)} a_i \cdot C_i\equals 1$, I believe that may actually be slower, since the fixed-base MSM should be much faster than the variable-base one and we do not have MSM algorithms that work on combinations of the two!
• Verifying $z$ is a size-$m$ inner product, so takes $\Fmul{m}+\Fadd{m}$

In total, we have $\Fmul{(2n + 3m)} + \Fadd{m} + \vmsm{n}{<p} + \fmsm{m}{<p}$ verifier work for vanilla $\hyrax$. The $\hyrax_\ipa$ variant would take $\Fmul{2(n+m)} + \vmsm{n}{<p} + \ipaVer(m)$ (because no decommitment check for $D$ and no $\A\cdot\b^\top$ inner-product).

When $(\x,\y)$ are on the hypercube: (1) $\a$ and $\b$ are 0 everywhere except at location $x$ and $y$, (2) $D$ is just the commitment $C_x$ to the $x$th row (3) $\A$ is verified directly against $C_x$ via an $\msm{m}$ (4) $z$ is verified by checking if $z \equals A_y$

Non-ZK performance

We use $\hyraxnm$ to refer to the $\hyrax$ scheme set up with $\hyraxSetup(1^\lambda, \log_2{n},\log_2{m})$. We use $\hyraxSqN$ to refer to $\hyrax^{\sqN,\sqN}$.

Setup, commitments and proof sizes

Non-ZK openings at arbitry points

Recall that $\emph{t}\le nm$ denotes the # of non-zero entries in the MLE $f$ or, equivalently, matrix $\mat{M}$.

Non-ZK openings at points on the hypercube

Conclusion

Your thoughts or comments are welcome on this thread.

References

For cited works, see below 👇👇