RSA Accumulators

An RSA accumulator is an authenticated set built from cryptographic assumptions in hidden-order groups such as $\mathbb{Z}_N^*$. RSA accumulators enable a prover, who stores the full set, to convince any verifier, who only stores a succinct digest of the set, of various set relations such as (non)membership, subset or disjointness. For example, the prover can prove membership of elements in the set to verifiers who have the digest.

The digest of the set is often referred to as the accumulator of the set.

RSA accumulators were introduced by Benaloh and de Mare¹ and later extended by Li et al.² with non-mmebership proofs. Recently, Boneh et al.³ extended RSA accumulators with many new features.

This post is not a full treatment of RSA accumulators, but will be extended over time.

Digest (or accumulator) of a set

Let $H$ be a collision-resistant hash function that maps its input to prime numbers. Let $g$ be the generator of a hidden-order group $\Gho$ where the Strong RSA problem is hard. Let $T = \{b_1, b_2, \dots, b_n\}$ and let $e_i = H(b_i)$ be the prime representative of $b_i$.

The accumulator of $T$ is:

\[a = g^{\prod_{i\in[n]} e_i}\]

Note that this can be computed in $O(n)$ exponentiations in $\Gho$.

Membership witnesses

To prove that $b_i$ is in the accumulator, a membership witness can be computed:

\[w_i = g^{\prod_{j\in[n]\setminus\{i\}} e_j} = a^{1/e_i}\]

Note that the witness is simply the accumulator of the set $T \setminus \{b_i\}$ and is just an $e_i$th root of $a$!

Unfortunately, computing this root cannot be done using an exponentiation by $1/e_i$ because $e_i$ cannot be inverted without knowing the order of the group $\Gho$. Instead, computing $w_i$ has to be done by exponentiating $g$ by the $n-1$ different $e_i$’s and thus takes $O(n)$ time, which can be slow. We explain below how this can be done in $O(\log{n})$ amortized time per witness.

To verify the witness against the accumulator $a$, one checks if:

\[a \stackrel{?}{=} w_i^{e_i}\]

In other words, one simply “adds back” $b_i$ to the set accumulated in $w_i$ and checks if the result equals $a$. This takes one exponentiation in $\Gho$.

Membership witnesses can be easily generalized into batch membership witnesses. For example, if one wants to prove that all $(b_i)_{i\in I}$ are in the accumulator, they can compute:

\[w_I = g^{\prod_{i\in[n]\setminus I} e_i} = a^{1/ \prod_{i\in I} e_i}\]

The verification proceeds analogously but takes $O(\vert I \vert)$ exponentiations:

\[a \stackrel{?}{=} w_i^{\prod_{i\in I}e_i}\]

Precomputing all membership witnesses fast

Computing all $n$ membership witnesses naively takes $O(n^2)$ exponentiations in $\Gho$, which does not scale well. Fortunately, Sander et al.⁴ give a divide-and-conquer approach for computing all witnesses which takes $O(n\log{n})$ exponentiations in $\Gho$.

The key observation is that half of the witnesses require computing $g^{\prod_{i\in[1,n/2]} e_i}$ while the other half require computing $g^{\prod_{i\in[n/2+1,n]} e_i}$. If done naively, these computations would be repeated many times unnecessarily. But one could compute the witnesses recursively in a tree-like fashion as follows ($n=8$ in this example):

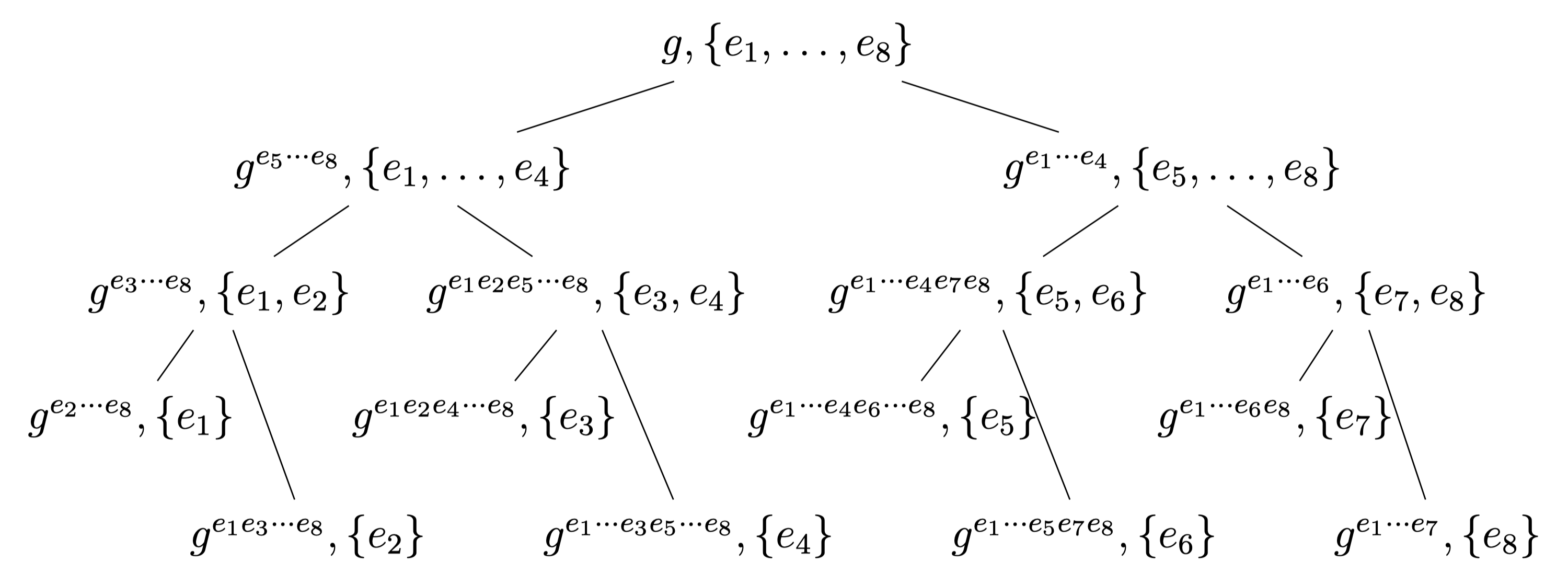
Intuition: You can think of each node as (1) a set of elements and (2) its batch membership witness w.r.t. the accumulator $a$. Then, this algorithm simply splits the set into two halves and disaggregates the witness into witnesses for the two halves. This repeats until witnesses for individual elements are obtained at the bottom.

In other words, this algorithm computes every $e_i$th root of $a$ (i.e., $g^{e_1 \dots e_{i-1} e_{i+1} \dots e_{n}}$) for all $i\in[n]$. The time to compute a tree of size $n$ leaves can be defined recursively as $T(n) = 2T(n/2) + O(n)$ because the amount of work done at the root of a size-$n$ subtree is $O(n)$ exponentiations plus the time to recurse on its two children. This gives $T(n) = O(n\log{n})$ exponentiations.

Boneh et al.³ baptised this algorithm as \(\rootfactor\). Specifically,

\[\rootfactor(g, (e_i)_{i\in[n]}) = (w_i)_{i\in[n]} = (a^{1/e_i})_{i\in[n]} = \left((g^{\prod_{j\in[n]} e_j})^{1/e_i}\right)_{i\in[n]}\]

More to come

There is so much more to be said about RSA accumulators! Hopefully, we will update this post over time with:

• Accumulator updates
• Membership witness updates
• Cross-incremental (dis)aggregation of membership witnesses⁵
• Non-membership witnesses
  • Updates
  • Aggregation
• Disjointness witnesses⁶
• Subset witnesses⁶