Catalano-Fiore Vector Commitments

A vector commitment (VC) scheme allows a prover with access to a vector $\mathbf{v} = [ v_1, \dots, v_n ]$ to convince any verifier that position $i$ in $\mathbf{v}$ stores $v_i$ for any index $i\in[n]$. Importantly, verifers only store a succinct digest of the vector (e.g., a 32-byte hash) rather than the full vector $\mathbf{v}$.

Below, we review Catalano and Fiore’s elegant VC scheme¹ built from hidden-order groups, extended with the enhancements proposed by Lai and Malavolta² and by Campanelli et al.³ We also make one new, small observation: proof disaggregation in this VC is faster than originally thought, which helps precompute all proofs slightly faster.

Preliminaries

Let $[n] = \{1,2,\dots, n\}$ and $[a,b] = \{a, a+1,\dots, b-1, b\}$.

We assume the reader is familiar with RSA accumulators, which Catalano-Fiore (CF) VCs rely heavily upon. Also, we assume familiarity with the $\rootfactor$ algorithm for computing all $e_j$th roots of $g^{\prod_{i\in[n]} e_i}, j\in [n]$.

Shamir’s trick

Given $z^{1/a}$ and $z^{1/b}$ where $z\in\Gho$ and $a,b\in\Z$ with $\gcd(a,b) = 1$, one can compute $z^{1/ab} = (z^{1/a})^y (z^{1/b})^x$ where $x,y$ are the Bezout coefficients for $a,b$ such that $ax+by=1$.

This is because:

\[(z^{1/a})^y (z^{1/b})^x = z^\frac{by}{ab} z^\frac{ax}{ab} = z^\frac{ax+by}{ab} = z^\frac{1}{ab}\]

We often use $z^\frac{1}{ab}\leftarrow \shamirtrick(z^{1/a}, z^{1/b}, a, b)$ to denote performing a Shamir’s trick..

Computing $z^{1/(ab)}$ takes \(O(\max(\vert x\vert,\vert y\vert))\ \Gho\) operations since the Bezout coefficients $(a,b)$ are as big as $(x,y)$. (Some extra time is needed to compute the Bezout coefficients, but we ignore it here.)

Public parameters

To set up the VC scheme, a hidden-order group $\Gho$ with generator $g$ must be picked such that nobody knows the order of the group. Importantly, the RSA problem needs to be hard in this group. Typically, $\Gho = \ZNs$ where $N=pq$ is picked via a secure multi-party computation (MPC) ceremony such that nobody knows the factorization of $N$ (and thus nobody knows the order of $\Gho$; i.e., $\vert\Gho\vert = \phi(N)= (p-1)(q-1)$).

Then, a collision-resistant hash function $H : [n] \rightarrow \primes^{\ell+1}$ must be fixe. $H$ will map each vector index $i\in [n]$ to a prime $e_i = H(i)$ such that $2^\ell < e_i < 2^{\ell+1}$ where $\ell$ is the maximum size in bits of a vector element $v_i$. We often use $e_K = \prod_{k\in K} e_k$ to denote a product of a subset of such primes, where $K\subseteq[n]$.

Digest (or commitments)

Instead of commitments, we’ll stick to the digest terminology.

The digest of a vector $\vect{v} = [ v_1, \dots, v_n ]$ consists of two parts. First, an RSA accumulator over all positions in the vector: \begin{align} S &= g^{\prod_{i\in[n]} e_i} \end{align}

Second, a multi-exponentiation of each RSA membership witness (w.r.t. $S$) for position $i$ to the value $v_i$: \begin{align} \Lambda &= \prod_{i\in [n]} (S^{1/e_i})^{v_i} \end{align}

We often use $d(\vect{v}) = (S, \Lambda)$ to denote the digest of a vector.

Computing the digest requires computing all $S^{1/e_i}, \forall i\in[n]$. As described before, this can be done in $O(n\log{n})$ group exponentiations via \((S^{1/e_i})_{i\in[n]} \leftarrow \rootfactor(g, (e_i)_{i\in[n]})\). Since each exponentiation is by an $(\ell+1)$-bit prime $e_i$, this takes $O(\ell n\log{n})\ \Gho$ operations. Then, $\Lambda$ can be computed with an additional $O(\ell n)\ \Gho$ operations.

The beauty of CF VCs is that, once you understand what a digest looks like, everything follows very naturally.

Proofs are just digests

At minimum, in any VC scheme, a verifier can be convinced of the value $v_i$ of any position $i$ in the vector using a proof $\pi_i$. To convince the verifier of multiple values $(\vect{v}_i)_{i\in I}$, this would require individual proofs for each position $i\in I$. However, in VCs like CF, a single $I$-subvector proof $\pi_I$ can be constructed for all $(v_i)_{i\in I}$. Importantly, the size of $\pi_I$ is always constant, independent of $\vert I\vert$.

In CF, an $I$-subvector proof $\pi_I$ is just the digest of the vector $\vect{v}$ but “without” positions $I$ in it. We abuse notation and denote this by \(\vect{v} \setminus I = (v_i)_{i\in[n] \setminus I}\). Thus, $\pi_I = d(\vect{v}\setminus I)$.

Let $e_I = \prod_{i\in I} e_i$. Then, the proof $\pi_I$ is just: \begin{align} S_I &= S^{1/e_I} = g^{\prod_{i\in[n]\setminus I} e_i}\\
\Lambda_I &= \prod_{i\in [n]\setminus I} (S_I^{1/e_i})^{v_i} \end{align}

Observe that the accumulator $S_I$ is over all positions $i$ except the ones in $I$. Also, observe that the membership witnesses in $\Lambda_I$ are w.r.t. to $S_I$ (not $S$) and that $\Lambda_I$ does not contain witnesses for $i\in I$. This is what it means to commit to a vector $\vect{v}$ “without” positions $I$ in it.

Computing $\pi_I$ takes $O(\ell(n-\vert I \vert)\log(n-\vert I\vert))\ \Gho$ operations, dominated by the cost to compute \((S_I^{1/e_i})_{i\in I}\) via \(\rootfactor(g, (e_i)_{i\in[n]\setminus I})\).

To verify the proof, one simply “adds back” \(\vect{v}_I\) to \(d(\vect{v}\setminus I) = \pi_I\) and checks it obtains the digest $d(\vect{v}) = (S, \Lambda)$ of the vector: \begin{align} S &\stackrel{?}{=} S_I^{e_I}\\
\Lambda &\stackrel{?}{=} \Lambda_I^{e_I} \prod_{i\in I} (S^{1/e_i})^{v_i} \end{align}

One problem is that all \((S^{1/e_i})_{i\in I}\) must be computed via \(\rootfactor(S_I, (e_i)_{i\in I})\), which would take $O(\ell \vert I\vert \log\vert I\vert)\ \Gho$ operations. We explain next how this can be done in $O(\ell \vert I \vert)\ \Gho$ operations by adding each $v_i, i\in I$ back into $\pi_I$ sequentially!

Updating digest

It is possible to update the digest $d(\vect{v})=(S,\Lambda)$ after an element $v_i$ changes to $v_i + \delta_i$. For this, the RSA membership witness $S^{1/e_i}$ is needed as helper information, which we refer to as an update key.

Since $S$ does not contain any information about $v_i$ (just about $i$), $S$ stays the same. However, $\Lambda$ must change into $\Lambda’$ as follows: \begin{align} \Lambda’ = \Lambda \cdot (S^{1/e_i})^{\delta_i} \end{align}

This technique can be generalized to work with many positions $i\in I$ changing by $\delta_i$. This either requires all the $S^{1/e_i}$ update keys or an aggregated update key \(S_I = S^{1/e_I} = S^{\prod_{i\in I} 1/e_i}\) as auxiliary information. In this last case, all the \((S^{1/e_i})_{i\in I} \leftarrow \rootfactor(S_I, (e_i)_{i\in I})\) can be computed in $O(\ell \vert I \vert \log \vert I \vert)\ \Gho$ operations from the aggregated update key. Then the update can be performed as \(\Lambda' = \Lambda \cdot \prod_{i\in I} (S^{1/e_i})^{\delta_i}\)

Adding new positions to the vector

It is also possible to “extend” the vector $\vect{v}$ of size $n$ to size $n+1$ by adding an extra element $v_{n+1}$. For this, the digest can be updated as: \begin{align} S’ &= S^{e_{n+1}}\\
\Lambda’ &= \Lambda^{e_{n+1}} S^{v_{n+1}} = \dots = \prod_{i\in [n+1]} (S’^{1/e_i})^{v_i} \end{align}

This can be generalized to adding $\Delta$ new positions, and would take $O(\ell \Delta)\ \Gho$ operations by applying each extension sequentially. In fact, this how one would verify a subvector proof fast: by adding back the elements being verified to the proof (which can be viewed as a digest) and checking the actual digest is obtained!

Updating proofs

Since proofs are just digests they are, in principle, updatable in the same fashion, with a few extra details.

Suppose we have a proof $\pi_I$ for a subvector \(\vect{v}_I\): \begin{align} S_I &= S^{1/e_I} = S^{1/\prod_{i\in I} e_i} = g^{\prod_{i\in[n]\setminus I} e_i}\\
\Lambda_I &= \prod_{i\in [n]\setminus I} (S_I^{1/e_i})^{v_i} \end{align}

Case 1: $i\in I$ changed

First, suppose a position $i\in I$ changes from \(v_i\) to \(v_i + \delta_i\). Then, the proof $\pi_I$ remains the same! This is because the proof contains no information about \(v_i\), since the proof is the digest of $\vect{v}$ without any positions $i\in I$.

Case 2: $j\notin I$ changed

Second, suppose a position $j\notin I$ changes from \(v_j\) to \(v_j+\delta_j\). In this case, we only need to change $\Lambda_I$ into a $\Lambda_I’$ such that: \begin{align} \Lambda_I’ = \Lambda_I \cdot (S_I^{1/e_j})^{\delta_j} \end{align}

The difficult part is computing $S_I^{1/e_j}$. We could do it from scratch but that would take $O(\ell (n - \vert I \vert))\ \Gho$ operations. Instead, as with the digest update, we assume we are given the $S^{1/e_j}$ update key associated with the changed position $j$. Fortunately, we know that we can compute $S_I^{1/e_j} = S^{1/(e_I e_j)}$ using Shamir’s trick on $S_I = S^{1/e_I}$ and $S^{1/e_j}$! (This takes $O(\ell \vert I \vert)\ \Gho$ operations which is faster when $|I|$ is much smaller than $n$.)

This technique can also be generalized to updating $\pi_I$ after many positions $j\in J$ changed by $\delta_j$. (Assume without loss of generality that $J\cap I =\varnothing$ or let $J \leftarrow J \setminus I$ otherwise.) This either requires all $S_I^{1/e_j}$ update keys or the aggregated update key \(S_{I\cup J} = S^{1/(e_I e_J)} = S^{\prod_{k\in I\cup J} 1/e_k}\) as auxiliary information. In this last case, all the \((S_I^{1/e_j})_{j\in J} \leftarrow \rootfactor(S_{I\cup J}, (e_j)_{j\in J})\) can be computed in $O(\ell \vert J \vert \log \vert J \vert)\ \Gho$ operations from the aggregated update key. Then, \(\Lambda_I' = \Lambda_I \cdot \prod_{j\in J} (S_I^{1/e_j})^{\delta_j}\).

Case 3: Adding new positions

Third, suppose a new position $v_{n+1}$ was added to the vector. Then the proof update proceeds similar to the digest update for adding new positions: \begin{align} S_I’ &= S_I^{e_{n+1}}\\
\Lambda_I’ &= \Lambda_I^{e_{n+1}} S_I^{v_{n+1}} = \dots = \prod_{i\in [n+1] \setminus I} (S_I’^{1/e_i})^{v_i} \end{align}

Disaggregating proofs

Suppose we want to disaggregate a proof $\pi_I=(S_I,\Lambda_I)$ for $\vect{v}_I$ into a proof $\pi_K=(S_K,\Lambda_K)$ for $\vect{v}_K$, where $K\subset I$.

In other words, we want to go from $d(\vect{v}\setminus I)$ to $d(\vect{v}\setminus K)$. Since $K\subset I$ we can write $K = I\setminus \Delta$ for some set $\Delta$ of indices. Thus, all we need to do is add back the elements from $\Delta$ to $\pi_I$.

So, for each $i\in \Delta$, we simply add back \((i,v_i)\) to \(\pi_I\) (as explained here) and obtain \(\pi_K\). This takes $O(\ell\vert\Delta\vert)$ $\Gho$ operations.

Aggregating proofs

To aggregate two subvector proofs for \(\vect{v}_I\) and \(\vect{v}_J\), things are bit more involved. Let \(\pi_I = (S_I,\Lambda_I)\) and \(\pi_J = (S_J,\Lambda_J)\) denote the two proofs. Assume that \(I\cap J = \varnothing\) and if not, just set \(J = J\setminus I\) and disaggregate \(\pi_J\) into \(\pi_{J\setminus I}\). (Can also set \(I=I\setminus J\) and disaggregate \(\pi_I\) instead.)

Denote the aggregated proof by \(\pi_{I\cup J} = (S_{I \cup J}, \Lambda_{I \cup J})\). We can easily compute the first part of the proof as:

\[S_{I\cup J} = \shamirtrick(S_I, S_J, e_I, e_J) = S^{1/(e_I e_J)}\]

For the second part, focusing on $\Lambda_I$, recall that: \begin{align} \Lambda_I &= \prod_{i\in [n]\setminus I} (S_I^{1/e_i})^{v_i} \end{align} We will tweak it as \(\Lambda_I^*\) by removing all elements $v_j, j\in J$ from \(\Lambda_I\): \begin{align} \Lambda_I^* &= \Lambda_I / \prod_{j\in J} (S_I^{1/e_j})^{v_j}\\
&= \prod_{i\in [n]\setminus (I\cup J)} (S_I^{1/e_i})^{v_i} \end{align} But for this, we need to compute \(S_I^{1/e_j},\forall j\in J\) via $\rootfactor$: \begin{align} (S_I^{1/e_j})_{j\in J} \leftarrow \rootfactor(S_{I\cup J}, (e_j)_{j\in J}) \end{align} In a similar, fashion, we can compute \begin{align} \Lambda_J^* &= \prod_{i\in [n]\setminus (I\cup J)} (S_J^{1/e_i})^{v_i} \end{align} Next, observe that \(\Lambda_I^*\) and \(\Lambda_J^*\) can be rewritten as: \begin{align} \Lambda_I^* &= \left(\prod_{i\in [n]\setminus (I\cup J)} (S^{1/e_i})^{v_i}\right)^{1/e_I}\\
\Lambda_J^* &= \left(\prod_{i\in [n]\setminus (I\cup J)} (S^{1/e_i})^{v_i}\right)^{1/e_J} \end{align} Thus, if we apply a Shamir trick on them, we can obtain $\Lambda_{I\cup J}$: \begin{align} \Lambda_{I\cup J} &= \shamirtrick(\Lambda_I^*, \Lambda_J^*, e_I, e_J)\\
&= \left(\prod_{i\in [n]\setminus (I\cup J)} (S^{1/e_i})^{v_i}\right)^{1/(e_I e_J)}\\
&= \prod_{i\in [n]\setminus (I\cup J)} (S_{I\cup J}^{1/e_i})^{v_i} \end{align}

Overall, if $b=\max(\vert I\vert, \vert J \vert)$, this requires Shamir tricks of size $b$ and $\rootfactor$’s of size $b$, so it takes $O(\ell b\log{b})\ \Gho$ operations.

Precomputing all proofs via disaggregation

Campanelli et al.³ explain how to compute all proofs fast via disaggregation. The idea is to start with a proof for the whole vector $\vect{v}$ and then disaggregate it into a proof for the left half of the vector and the right half. Then, one repeats recursively on these two halves. This determines a tree of subvector proofs, where the leaves store the proofs for the individual vector and each internal node stores an aggregation of its children’s proofs (with the root storing the proof for the full vector).

Here’s an example for $n=8$:

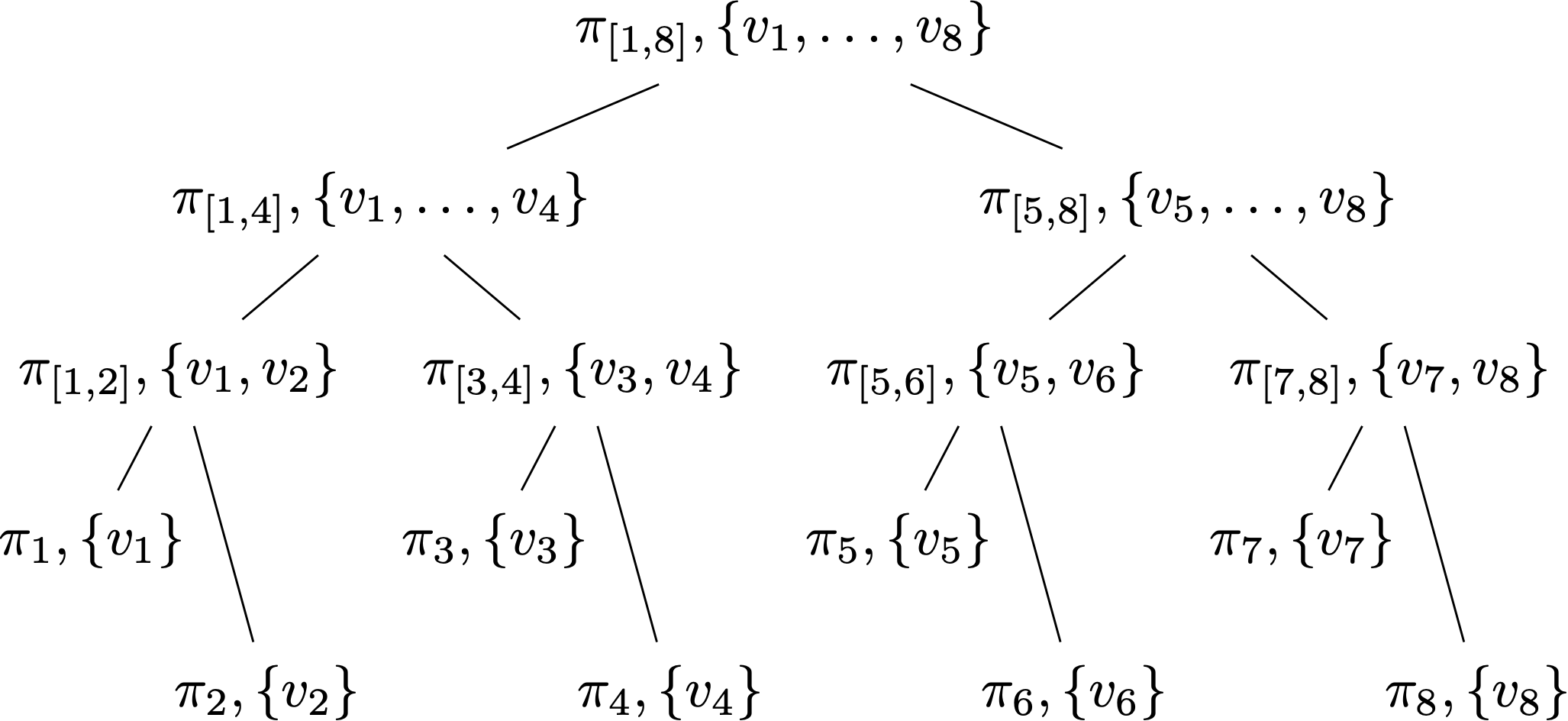
Looked at it differently, clearly one can compute this tree via proof aggregation, which we discuss next, by starting with the leaves storing individual proofs for each position $i$ and aggregating up the tree. The key observation is that one can also compute this tree by starting with the root, which stores the proof for the full vector (i.e., the empty digest), disaggregating this proof into two halves, and recursing on these two halves.

This very much resembles the recursion tree used to implement $\rootfactor$ efficiently (see here). Indeed, if you think about it, this tree implicitly computes the $\rootfactor$ tree too, since each CF proof for $v_i$ has an RSA membership witness for $i$ in it.

Note that Campanelli et al.³ claim $O(\ell n\log^2{n})\ \Gho$ operations for this algorithm, but the faster disaggregation explained above actually gives $O(\ell n\log{n})$.