Keyless blockchain accounts on Aptos

tl;dr: What is a keyless blockchain account? Put simply, “Your blockchain account = Your Google account”. In other words, this keyless approach allows you to derive a blockchain account from any of your existing OpenID Connect (OIDC) account (e.g., Google, Apple), rather than from a traditional secret key or mnemonic. There are no long-term secret keys you need to manage. There is also no multi-party computation (MPC) system managing your account for you. As a result, the risk of account loss is (more or less), the risk of losing your Google account. Keyless is built using a Groth16 zero-knowledge proof to maintain privacy in both directions: prevent the blockchain from learning anything about your Google account & prevent Google from learning anything about your blockchain account and transaction activity.

One day, I hope to edit this into a full blog post but, until then, here’s a bunch of resources.

tl;dr

A quick 20 minute presentation on what this is & how it works:

FAQ

Who is this for?

So far, cryptocurrencies have been designed for power users who understand public-key cryptography.

In constrast, Keyless accounts are for any Web 2 user who has used the “Sign in with Google¹” flow before. (Basically, for everyone.)

Keyless accounts are primarily designed for the bottom 90% of users; novice users who are not yet ready to manager their own 12-word seed phrase, mnemonic or secret key.

Such users often tend to:

• lose their key, or
• get phished for their key, or
• accidentally-paste their key somewhere they shouldn’t

But, keyless accounts were designed also for first-time users, who deserve and expect a smooth on-boarding experience when interacting with a dapp.

Newsflash: Downloading a new wallet for every new chain and writing down a new (extremely-sensitive) 12-word seed phrase is not smooth. (It’s not even sane.) Reusing an existing 12-word seed phrase is not smooth either. Plus, would you want to? Do you trust this new wallet on this new chain?²

Can Google steal my keyless account?

In principle, keyless accounts can be set up so that, if a malicious Google tries to steal your account, you have the power to stop it by sending a cancellation TXN within a timeout period (e.g., 1 day)³.

In practice though, this higher-security mode of operation will not lead to the best user experience (e.g., across different devices⁴ or when a user’s browser session is lost⁵). As a result, this is not the recommended mode on the Aptos network, nor the most-widely supported one.

Instead, Aptos defaults to a user-friendly mode where users can access their account easily from different devices (even if the browser’s history has been cleaned). For this to work, Google must be allowed to sign TXNs on the user’s behalf without a timeout period (see flow). As a result, a malicious (or compromised) Google could abuse this power and steal a user’s account.

Is this okay? Well, you have to remember who keyless accounts are for.

First, they are for first-time users who are not interested in (or know much about) 12-word mnemonics; they just want to easily sign up for your your dapp! Second, they are for novice users who understand very little about the responsibility of custodying a 12-word seed phrase or mnemonic.

So, yes, this is okay, because the biggest threat for this user base is key loss (or theft) caused by the user themselves. It’s not Google.

Then, as a developer, if you want to (1) on-board users smoothly and (2) prevent them from shooting themselves in the foot, then you should use keyless⁶.

Put differently, Google can protect these users’ keyless accounts much, much better than the users are able to secure a 12-word seed phrases.

Google’s own bottom line depends on their ability to protect their OpenID Connect (OIDC) secret keys which secure your keyless account because those same keys secure the widely-used “Sign in with Google” flow all across the web!

Drawings

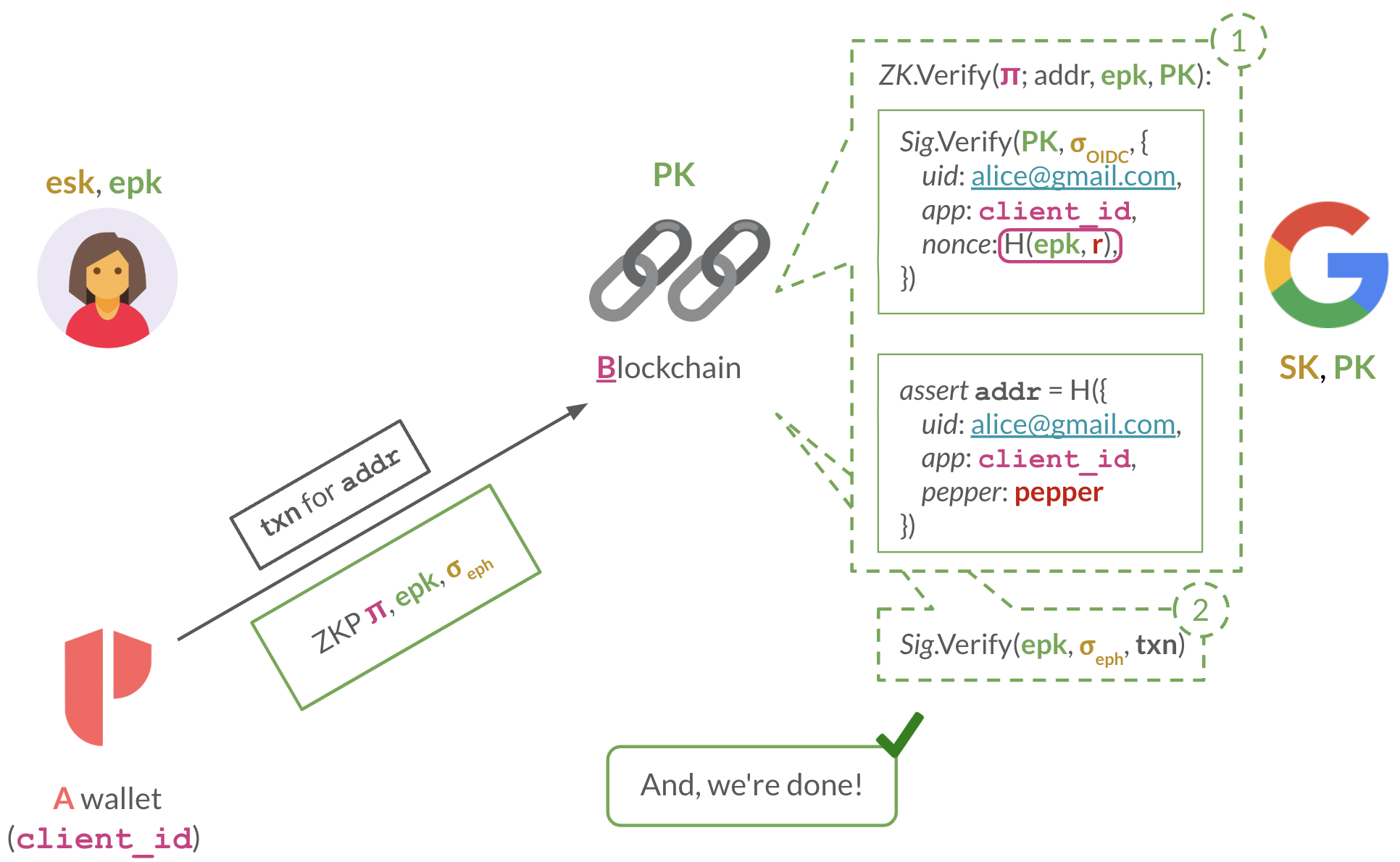
Flow: Keyless on-chain verification

Depicts what the blockchain validators need to do to verify a keyless TXN submitted by a user, Alice.

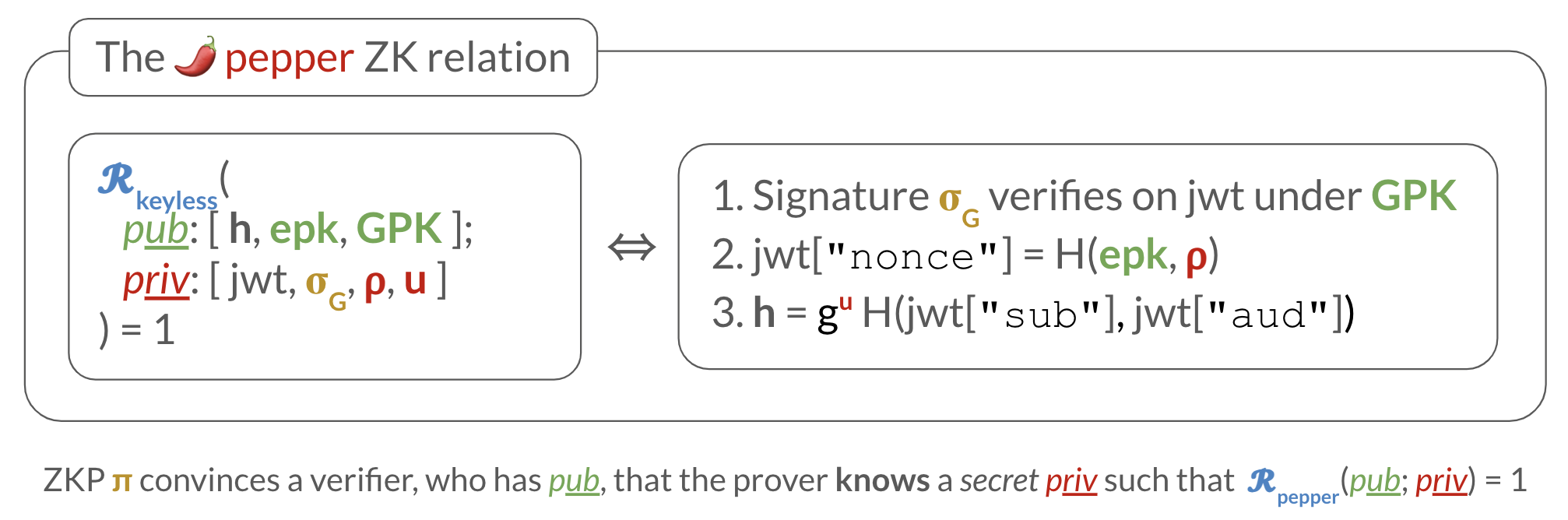
ZK relation: Keyless authentication

10,000-feet view of the ZK relation needed for keyless:

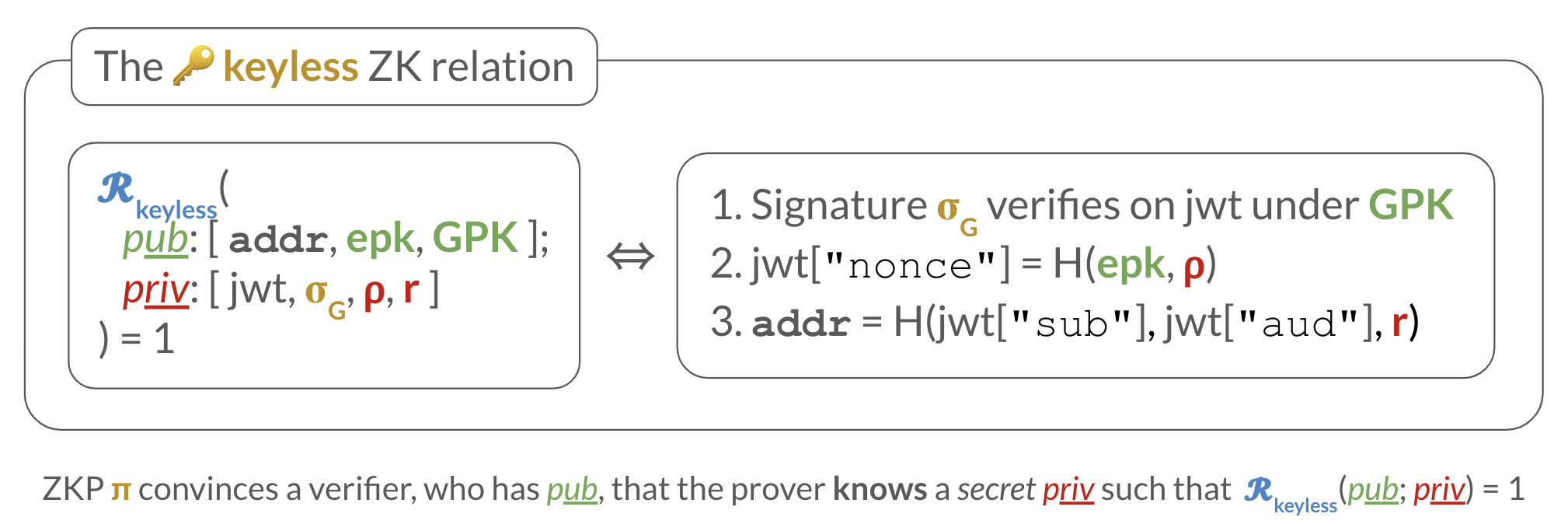
For a 100-feet view of it, see this AIP-61 sub-section.

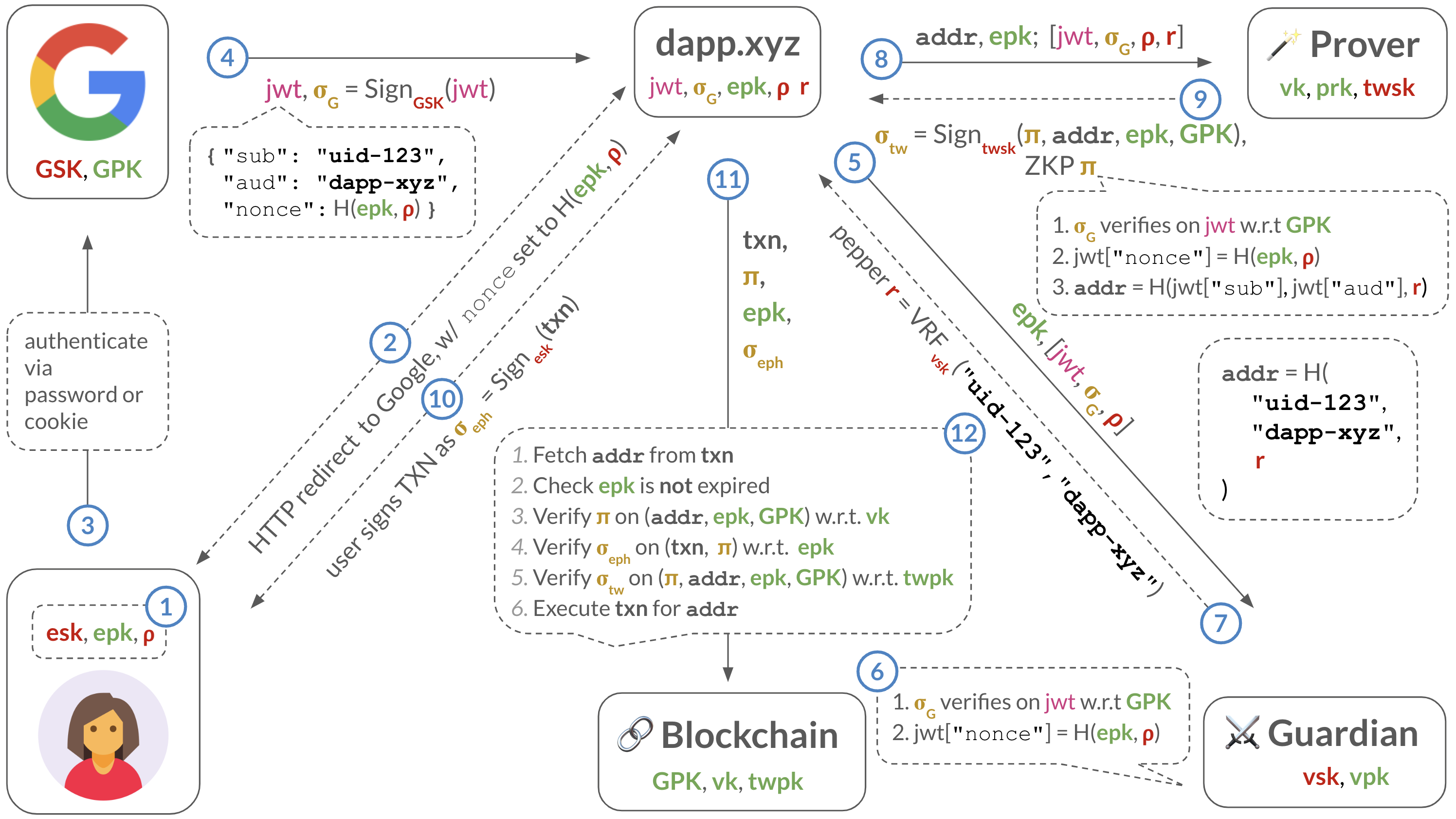
Flow: End-to-end keyless transacting

Depicts the full keyless flow: the user generating an ESK and EPK, the user signing into the dapp with the EPK as the OIDC nonce, the dapp getting a JWT, exchanging it for a pepper, getting a ZKP from the prover service, the user signing a TXN with their ESK, the dapp sending the TXN containing the ZKP and ephemeral signature, and finally the blockchain verifying everything.

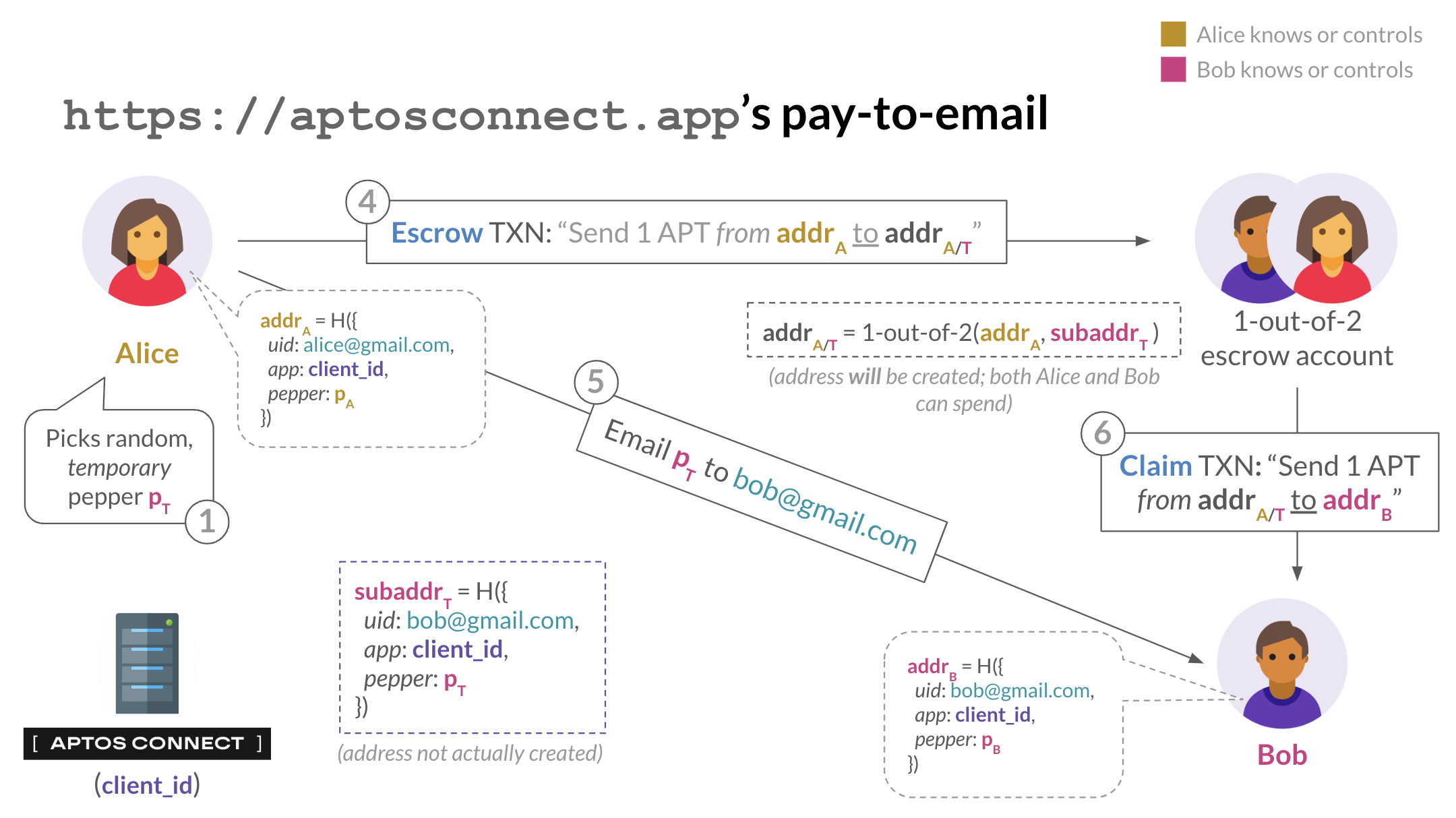
Flow: Paying an email address via https://aptosconnect.app

Flow: End-to-end keyless ZKless-transacting (currently, disabled)

In case of emergency (e.g., a serious soundness issue in the ZK circuit), keyless supports a ZKless mode that is not privacy preserving. This, of course, is currently disabled on Aptos mainnet.

We depicts this (simpler) ZKless flow: the user generating an ESK and EPK, the user signing into the dapp with the EPK as the OIDC nonce, the dapp getting a JWT, the user signing a TXN with their ESK, the dapp sending the TXN containing the ephemeral signature, and finally the blockchain verifying everything.

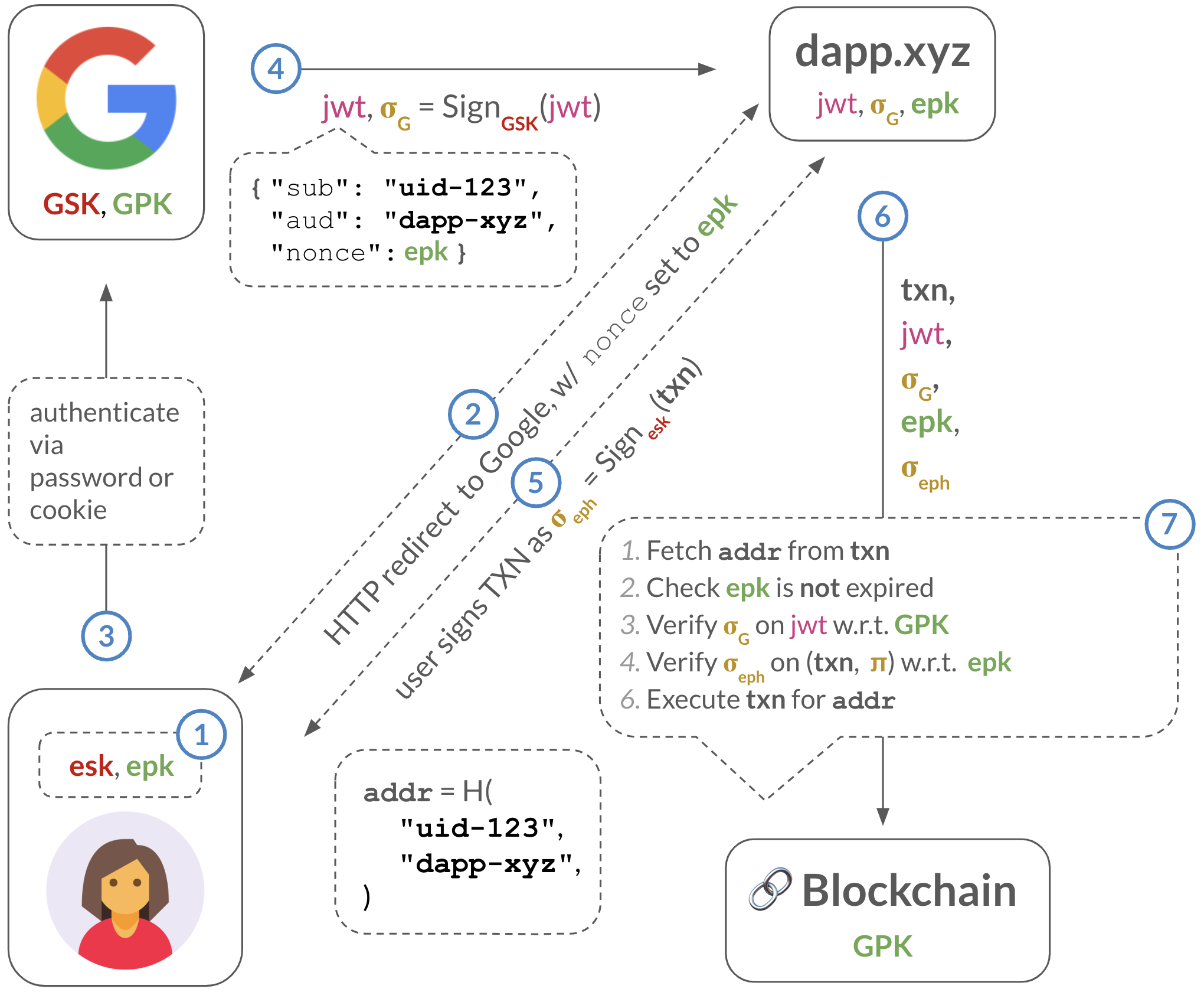
ZK relation: Oblivious pepper service

The ZK relation needed to implement an oblivious pepper service:

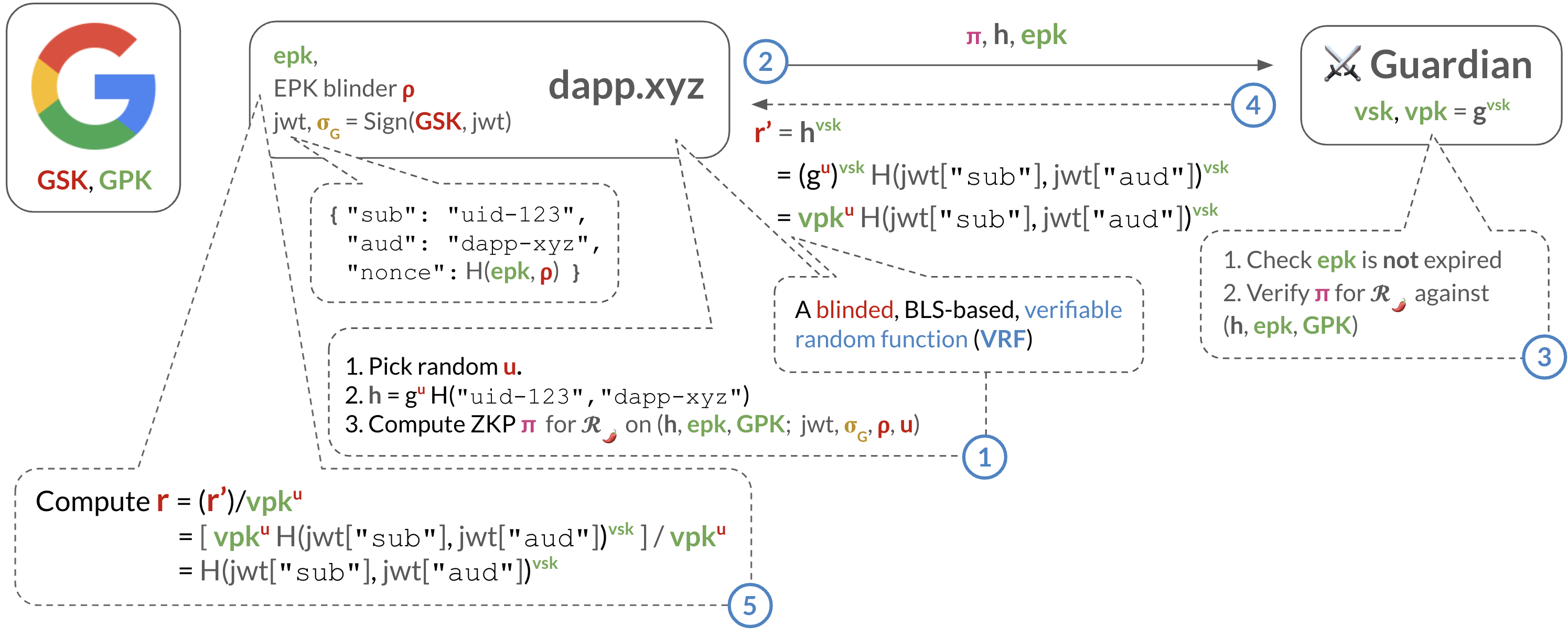
Flow: Fetching your pepper obliviously

We depict the flow for a dapp to fetch its user’s pepper obliviously from the pepper service, without leaking the user’s ID nor the application’s ID to the service.

Write-ups

1. I wrote a high-level overview of how keyless accounts work on the Aptos blockchain
2. I wrote an in-depth explanation of how keyless accounts work (and their many caveats) in the 61st Aptos Improvement Proposal.
3. Osikhena Oshomah wrote a keyless tutorial for devs called Aptos Keyless Auth

Slides

• Keyless blockchain accounts from ZKPs, MIT and Northeastern University, February 2025
• Keyless blockchain accounts from ZKPs, NoirCon 1, February 2025
• Keyless blockchain accounts from ZKPs, GKR bootcamp, January 2025
• How Keyless works, 2024-2025
• Aptos Keyless accounts, zkSummit’11, April 2024

Code

• Keyless blockchain validator logic here
• Keyless governance logic here
• Keyless prover service here
  • Built on top of our own rust-rapidsnark
  • Which, in turn, is built on top of our own hardened rapidsnark
• Keyless ZK circuit circom code here
• Keyless pepper service here
• Keyless TypeScript SDK here

Educational (d)apps and code

• Example: Sending a keyless TXN to the Aptos mainnet via the SDK here
• Example: Simple Keyless dapp on Aptos here with guide here
• Example: Federated keyless dapp on Aptos here
• Example: End-to-end dapp with Keyless here with guide here

Deployed applications

1. Aptos Connect web-wallet
2. $\Rightarrow$ every Aptos dapp that can connect a wallet!
3. Merkle Trade

Aptos Improvement Proposals (AIPs)

AIP for the whole keyless design:

• AIP-61: Keyless accounts

AIPs for auxiliary keyless services:

• AIP-75: Prover service
• AIP-81: Pepper service
• AIP-67: Native JWK consensus

AIPs for recent extensions to keyless:

• AIP-96: Federated Keyless
  • Adds decentralized support for “federated” OIDC providers like Auth0, which have tenant-specific iss’s and JWKs and could not be scalably integrated into our JWK consensus mechanism
• AIP-108: “Audless” Federated Keyless
• Draft AIP: Oblivious pepper service

Tweets

A tweetstorm summarizing Aptos Keyless can be found below:

What is an @aptos keyless account? 🧵

It's a blockchain account derived from (say) your Google account and an application (wallet, dapp, etc).

It's bound not just to you (e.g., you@gmail.com) but also to the application (e.g., @PetraWallet, or @ThalaLabs, or @VibrantXFinance) pic.twitter.com/L3qgRf1WoS

— Alin Tomescu (@alinush407) June 12, 2024

Presentations

zkSummit’11 (2024)

In April 2024, I gave a 20-minute presentation at zkSummit11.

Go back up to see it!

GKR bootcamp (2025)

In January 2025, I gave a 1 hour bootcamp on keyless accounts:

NoirCon 1 (2025)

In February 2025, I gave a 25 minute workshop on keyless accounts at AZTEC’s NoirCoin 1:

Future work

Noir

• Groth16 experimental gnark backend
• Noir-to-R1CS experimental
• Benchmarking individual Noir functions

Miscellaneous

• Code: AnonAdhar, by PSE, does RSA2048-SHA2-256 signature verification in circom within ~900K R1CS constraints

Apendix

This will serve as an appendix of technical information, useful when communicationg about keyless accounts internally and externally.

The notation below will not be explicitly defined; just exercise intuition! e.g., $\maxaudval$ is clearly the maximum number of bytes in $\audval$.

BN254

Currently, the Aptos keyless relation is implemented using circom with a Groth16 backend over the BN254 elliptic curve⁷ of order $r$, where $2^{253} < r < 2^{254}$:

\begin{align} & 2^{253} + 2^{252} + 2^{246} + 2^{245} + 2^{242} + 2^{238} + 2^{235} + 2^{234} + 2^{233} + 2^{230} + 2^{229} + 2^{228} + 2^{225} +\\
& 2^{223} + 2^{222} + 2^{221} + 2^{216} + 2^{213} + 2^{212} + 2^{208} + 2^{207} + 2^{205} + 2^{197} + 2^{195} + 2^{192} + 2^{191} +\\
& 2^{189} + 2^{188} + 2^{187} + 2^{182} + 2^{180} + 2^{174} + 2^{170} + 2^{168} + 2^{167} + 2^{165} + 2^{164} + 2^{162} + 2^{161} +\\
& 2^{159} + 2^{152} + 2^{151} + 2^{144} + 2^{142} + 2^{140} + 2^{139} + 2^{134} + 2^{132} + 2^{131} + 2^{130} + 2^{128} + 2^{125} +\\
& 2^{123} + 2^{117} + 2^{116} + 2^{113} + 2^{112} + 2^{111} + 2^{110} + 2^{109} + 2^{107} + 2^{102} + 2^{99 } + 2^{94 } + 2^{93} + \\
& 2^{92 } + 2^{91 } + 2^{88 } + 2^{87 } + 2^{85 } + 2^{84 } + 2^{83 } + 2^{80 } + 2^{78 } + 2^{77 } + 2^{76 } + 2^{71 } + 2^{68} + 2^{64} + 2^{62} +\\
& 2^{57 } + 2^{56 } + 2^{55 } + 2^{54 } + 2^{53 } + 2^{48 } + 2^{47 } + 2^{46 } + 2^{45 } + 2^{44 } + 2^{42 } + 2^{40 } + 2^{39} + 2^{36} + 2^{33} +\\
& 2^{32 } + 2^{31 } + 2^{30 } + 2^{29 } + 2^{28 } + 2^0 \end{align}

In decimal, $r$ is 21888242871839275222246405745257275088548364400416034343698204186575808495617. In hexadecimal, $r$ is 0x30644e72e131a029b85045b68181585d2833e84879b9709143e1f593f0000001.

The base field where the elliptic curve point coordinates $(x,y)$ lie in is $\Zp$ with $p = $ 21888242871839275222246405745257275088696311157297823662689037894645226208583. Note that $p$ is slightly larger than the elliptic curve’s order $r$.

base64url

Recall that base64 is a way to convert an input of $\ell$ bytes into an output of $m=\lceil 4\ell / 3\rceil$ base64 characters from an alphabet of size 64.

Base64 works by sequentially converting each group of 6 bits (so $2^6 = 64$ possibilities) to an 8-bit letter in this base64 alphabet. Note that this blows up the encoded length by around $8/6 = 4/3 = 1.25\times$.

Why base64-encode stuff? Because it is sometimes useful to take arbitrary bytes and convert them to a displayable string format. (For example, hexadecimal is another such format, albeit the conversion.

The base64 algorithm encodes every 24-bit input chunk (i.e., every 3 bytes) into a 32-bit output chunk (i.e., 4 base64 characters), properly handling things when $\ell \bmod 3 \ne 0$ (see this Wikipedia article):

Specifically, the last input chunk could be of either length:

• $\ell \bmod 3 = 2$ bytes
  • then, the algorithm pads this last 2-byte input chunk (16 bits) with 2 zero bits
    • the padded chunk’s length is now 18 bits and thus divisible by 6
  • encode this 18-bit padded input chunk as 3-character output chunk
  • append an = padding character to the output chunk
    • to indicate that the last 2 zero bits in the padded input chunk are padding bits and should be removed
• $\ell \bmod 3 = 1$ bytes
  • same, except pad this last 1-byte chunk (8 bits) to 12 bits using 4 zero bits
  • as a result, append two = padding characters to the resulting 2-character output chunk.

Padding is actually not necessary since it can be inferred from the output length: i.e., the output length $m \bmod 4$ can be either $0, 2$ or $3$, in which case we can show that $\ell \bmod 3$ must have been either $0, 1$ or $2$, respectively⁸. Indeed, some implementations do omit it (e.g., base64url-encoded JWTs and JWSs).

Now, base64url is a slight varation on base64: as explained in the JWS RFC⁹. Specifically, base64url(m) is implemented by:

1. Doing a vanilla output = base64(input) Base64 encoding
2. Stripping the padding (=) characters at the end of output, if any
3. Replacing + with - and replacing / with _ in output

Hashing the identity commitment (IDC) in the address

\begin{align} \addridc \bydef \poseidon^\F_4\left( \begin{array}{l} \pepper[0..30],\\
\poseidon^\mathbb{S}_{\maxaudval}(\audval),\\
\poseidon^\mathbb{S}_{\maxuidval}(\uidval),\\
\poseidon^\mathbb{S}_{\maxuidkey}(\uidkey)\\
\end{array} \right) \end{align}

Define $\poseidon^\mathbb{S}_\ell(s)$.

Strings inside ZK circuits

• String indices start at 0:
  • $s[0]$ is the first character of $s$
  • $s[\len(s) - 1] \bydef s[-1]$ is the last character of $s$.
• $s[i : j] \bydef \left[ s[0], s[i+1], \ldots, s[j] \right]$ denotes a substring starting at $i$ and ending at $j$ (inclusive).
• No characters in $s[0:\len(s)-1]$ can be 0 (or null).
• A string is zero-padded up to its max length, denoted by $\maxlen(s)$: i.e., $s[\len(s):\maxlen(s) - 1] = [0,\ldots,0]$

Substring checks from polynomial checks

The inputs are:

• a string $s$ of max length $N$ and actual length $\len(s) = n\le N$
• a substring $t[0\ldots L]$ of max length $L$ and actual length $\len(t)=\ell\le L$
• a starting index $i\in [0,n)$ of $t$ in $s$

The output is a bit indicating that the following are all true:

1. $0 < \ell \le n$¹⁰
2. $i < n - (\len(t) - 1)$ (we need to “leave room” for $t$ in $s$)
3. $s[i:i+\len(t)-1] = t$ (i.e., $t$ is a substring of $s$ starting at index $i$)

Interactive protocol

Can we avoid bitmasks here?

Non-interactive via Fiat-Shamir (FS)

Interactive + FS.

$$ \def\Adv{\mathcal{A}} \def\Badv{\mathcal{B}} \def\vect#1{\mathbf{#1}} $$

References

For cited works, see below 👇👇