Complete vs. full vs. perfect binary trees

tl;dr: The terms full, complete, and perfect binary tree are often confused with each other. In this short post, we define each one, give examples, and work out all the relationships between them — including the perhaps-surprising fact that full + complete does not imply perfect.

Real quickly, the Venn diagram below shows how the three classes relate to each other: Perfect is a strict subset of Full $\cap$ Complete.

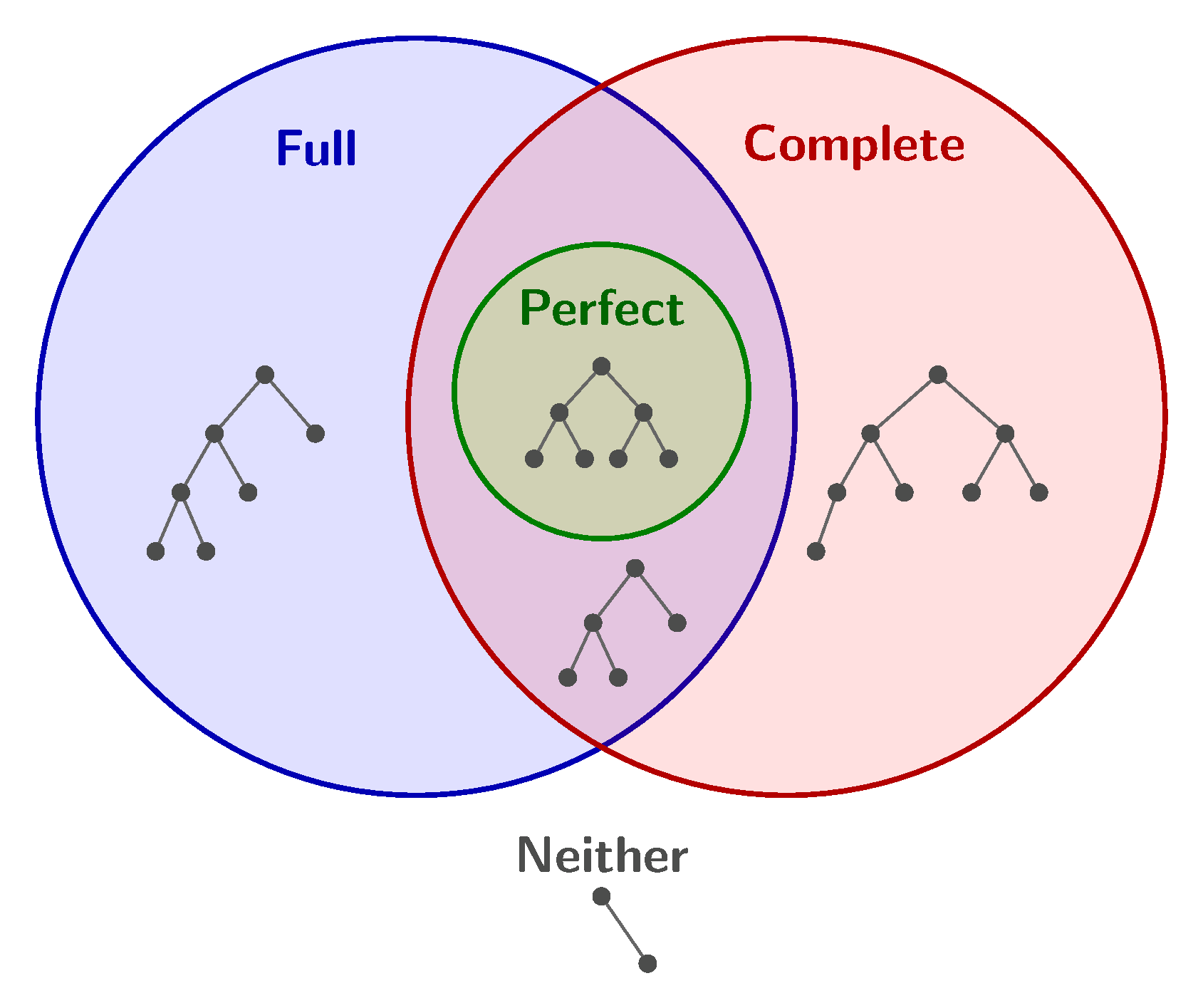
Definitions

Full binary tree

A full (a.k.a., proper or strict) binary tree is one where every node has 0 or 2 children. In other words, no node has exactly one child.

Example 1 — A single node (trivially full):

graph TD
    A(( ))

Example 2 — A 5-node full tree:

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    C --- D(( ))
    C --- E(( ))

Example 3 — A 7-node full tree that is not perfect (leaves at depths 1, 2, and 3):

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- E(( ))
    D --- F(( ))
    D --- G(( ))

Complete binary tree

A complete binary tree must have two properties:

1. Every level is fully-filled except possibly the last,
2. The last level is filled from left to right.

This is the shape you get when you insert elements into a binary heap one by one.

Example 1 — A 4-node complete tree (note: not full, since the left child has only one child):

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- inv[ ]

    style inv fill-opacity:0, stroke-opacity:0;
    linkStyle 3 stroke:none;

Example 2 — A 5-node complete tree (this one is also full):

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- E(( ))

Example 3 — A 6-node complete tree (note: not full, since the right child has only one child):

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- E(( ))
    C --- F(( ))
    C --- inv[ ]

    style inv fill-opacity:0, stroke-opacity:0;
    linkStyle 5 stroke:none;

Perfect binary tree

A perfect binary tree must have two properties:

1. All internal nodes have exactly 2 children,
2. All leaves are at the same depth.

A perfect binary tree of height $h$ has exactly $2^{h+1} - 1$ nodes.

Example 1 — Height 0 (1 node):

graph TD
    A(( ))

Example 2 — Height 1 (3 nodes):

graph TD
    A(( )) --- B(( ))
    A --- C(( ))

Example 3 — Height 2 (7 nodes):

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- E(( ))
    C --- F(( ))
    C --- G(( ))

---

Relationships

There are six pairwise implications to consider. Let’s work through all of them.

Full $\nRightarrow$ Complete

Counterexample: this tree is full (every node has 0 or 2 children), but not complete because the second level is not filled from left to right — the right subtree is deeper than the left.

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    C --- D(( ))
    C --- E(( ))

Full $\nRightarrow$ Perfect

Counterexample: this full tree has leaves at depths 1 and 3, so it is not perfect.

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- E(( ))
    D --- F(( ))
    D --- G(( ))

Complete $\nRightarrow$ Full

Counterexample: this 4-node complete tree has a node with exactly one child, violating fullness.

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- inv[ ]

    style inv fill-opacity:0, stroke-opacity:0;
    linkStyle 3 stroke:none;

Complete $\nRightarrow$ Perfect

Counterexample: this 5-node complete tree has leaves at depths 1 and 2.

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- E(( ))

Perfect $\Rightarrow$ Full

By definition, every internal node of a perfect tree has exactly 2 children, which is exactly the requirement for fullness.

Perfect $\Rightarrow$ Complete

In a perfect tree, every level is completely filled (including the last). This trivially satisfies the definition of completeness.

Full + Complete $\nRightarrow$ Perfect

Many people assume that if a tree is both full and complete, then it must be perfect. This is false.

Counterexample: Consider this 5-node tree.

graph TD
    A(( )) --- B(( ))
    A --- C(( ))
    B --- D(( ))
    B --- E(( ))

• Full? Yes — every node has 0 or 2 children. ✅
• Complete? Yes — levels 0 and 1 are fully-filled, and level 2 is filled from the left. ✅
• Perfect? No — level 2 is not fully-filled $\Rightarrow$ all leaves are not at the same depth ❌

The key insight is that completeness only requires the last level to be left-filled; it does not require the last level to be fully filled. And fullness only bans single-child nodes; it says nothing about leaf depths. Combined, the two properties are still not strong enough to force all leaves to the same depth.

When does full + complete $=$ perfect?

When the number of nodes $n = 2^{h+1} - 1$ for some $h$ (i.e., the last level is fully-filled). In that case — and only that case — a complete tree is also perfect (and, trivially, also full).

---